難問の墓場
最終更新日：2025年3月6日
難問の墓場にようこそ（2024/4/4 開園）
難易度が高すぎて使い道がなくなった残念な問題たちの墓場です。興味があれば供養して（解いて）あげてください。下部の解答送信フォームから解答を送ることができます。返信はいたしませんが、正解していれば正解者のニックネームを掲載いたします。ページが更新されても正解者に追加されていなければ、正解の条件を満たしていなかったということです。不定期に問題を追加いたします。解答の過程は適当に省略しながらでかまいませんが、肝心なところは省略しないでください。もし書ききれなければ何回かに分けて送信してください。繁忙期は更新までお時間をいただきます。質問や苦情などはご遠慮ください。
そのうち問題が発生してページを削除しそうな予感がしています。ご容赦ください。
正解の条件（すべて満たす必要があります）
１．答えが合っている。
２．解答の過程が論理的に正しいと墓守が理解できる。
３．解き方の条件を満たしている。
４．ニックネームが不適切でない。
５．解答の過程が最近のものとよく似たものでない。
正解のはずなのに正解者に追加されない場合はどこかの条件に引っかかっていると思われます。
２については墓守の理解を超えているのかもしれません。高校数学の教科書に載っていそうな範囲でやさしく書いてください。
４については適当に名前を変えてみてください。
５については一週間ほどしてから再度送信してください。
解き方の条件について
中学受験算数：相似形の性質（辺の比、面積比）は使用可。三平方の定理などは証明を利用して強引に解くのも不可。
正解者について
ニックネームの後に「さん」をつけています。また、私の想定より良い解答のうち、最も良い解答だった人のニックネームの前に「＊」をつけています。
１．循環小数（2024/4/4 掲載 想定対象：小５以上）【算数/数学】
次の分数を小数に直したとき、小数第100位の数は何か。
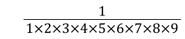
解き方の条件：高校数学まで。途中経過必須。
正解者：ウェザエモンさん
２．弓形の面積（2024/4/6 掲載 想定対象：小６以上）【算数】
図のように、点 O を中心とする円が四角形 ABCD の４つの頂点を通っている。四角形 ABCD の対角線 AC と BD は点 E で垂直に交わっていて、AE＝112、BE＝84、CE＝12、DE＝16、CD＝20 である。図の色をつけた２つの部分の面積の和を求めよ。円周率は3.14とする。
解き方の条件：中学受験算数まで。
正解者：＊ウェザエモンさん
３．ピタゴラス三角形（2024/4/6 掲載 2025/3/6修正 想定対象：中３以上）【数学】
すべての辺の長さが自然数である直角三角形はピタゴラス三角形と呼ばれている。長さ n（nは3以上の自然数）の辺を持つピタゴラス三角形の中で面積が最大のものについて、その面積を求めよ。
※ n を具体的な３桁の自然数として解いても正解とします。
解き方の条件：高校数学まで。
正解者：正解者はまだいません。
墓守より：答えが大きすぎるかなと思って修正しました（修正前は n = 2024 ）。答えを n で表すのは数Ⅰを勉強してからがいいと思います。
４．三角形の面積（2024/4/4 掲載 想定対象：小６以上）【算数】
AB＝13、BC＝14、CA＝15である三角形ABCの面積を求めよ。
解き方の条件：中学受験算数まで。
正解者：正解者はまだいません。
墓守より：三平方の定理と同様に直角三角形の三辺の比（3：4：5など）も使用不可です。相似形の相似比と面積比の関係は使ってOKです。一応中学受験算数の知識で解けますが、実際に解ける小学生がいるのか微妙なので、小学生の皆さんは時間を使い過ぎないようにしてください。
５．二〇二四芒星（2024/10/31 掲載 想定対象：高１以上）【数学】
ともに点 O を中心とする半径 1 の円 O1 と、半径 r ( r < 1 )の円 O2 がある。O1 の周上に点 A0 をとり、A0 から O2 に接線を 1 本引いて、これが再び O1 と交わる点を A1 とする。以下同様に、Ak ( k = 1, 2, 3, … ) から新たに O2 に引いた接線が再び O1 と交わる点を Ak＋1 として順に点をとっていくと、A2024 がはじめて A0 と一致した。このような r の値は複数あり、小さい方から順に r1, r2, r3, …, rn とする。
r12 + r22 + r32 + … + rn2 の値を求めよ。
解き方の条件：高校数学まで。
正解者：正解者はまだいません。
６．電気振り子（2024/11/26 掲載 想定対象：高３以上）【物理】
絶縁体のひもの一端に重さ 0.10 N の小球をつけ、他端を固定して小球が自由にふれるようにした。小球に 4.0×10-5 C の電荷を与え、空間全体に 7.0×102 V/m の一様な電場を加えたところ、小球が鉛直線から θ 傾いて静止した。一様電場の強さを一定に保ち、その向きをさまざまな向きにゆっくりと変えながら小球が静止する θ の値を測定したところ、ある向きのときに θ の値が最大値 θ0 となった。
tan θ0 の値を有効数字 2 桁で求めよ。
解き方の条件：なし（今のところ）
正解者：正解者はまだいません。
解答送信フォーム
※ 墓参者名は常識的にアウトなもの、本名と思えるものは禁止です。ギリギリを攻めるのもやめてください。